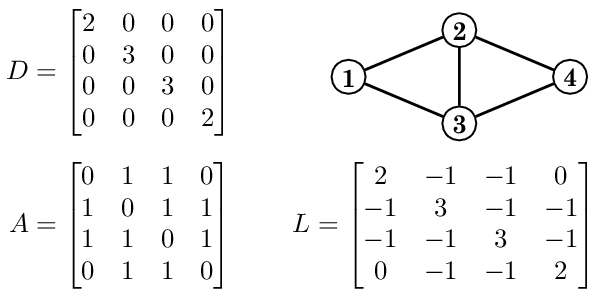
GCN 논문을 review하고 난 후 이어서 바로 deep-dive를 했던 논문.
소개된 모델의 이름에 SAGE(현자)가 들어가있어서 좀 신기하기도 하고 피식했던 기억이 난다.
GCN과 마찬가지로 원본 코드가 tensorflow v1으로 작성되었던 터라 코드 분석과 실행에 다소 애를 먹었지만, 그래도 개인적으론 (appendix 부분을 제외하고) GCN에 비해 수학적 background가 많이 요구되었던 것 같지는 않았다.
논문에서 계속 GCN을 언급하면서 GCN을 확장했다, GCN보다 성능이 잘 나온다 라는 말이 나오는데, GCN paper review는 이전 포스팅에서 확인할 수 있다.
Published in NIPS(NeurIPS)2017
Transductive한 방법으로 접근한 이전 연구들과는 다르게 Inductive한 방법으로 접근하는 방법을 소개.
지역적인 이웃(local neighborhood)들의 feature를 적절하게 sample & aggregate하여 node embedding을 생성하는 함수를 학습하는 방법을 소개.
random neighborhood sampling을 활용한 mini-batch training 방법을 소개.
Introduction
node2vec, DeepWalk, LINE과 같은 이전 representation learning 방법들은 large graph의 node를 low-dimensional embedding vector로 변환하여 여러 downstream task를 위한 입력을 준비하는데 사용되었다.
여기서의 핵심인 node embedding은 기본적으로 차원 축소(dimensionality reduction technique), 즉 high-dimensional인 node의 이웃 정보를 low-dimensional인 dense embedding vector로 압축하는 것.이를 통해 여러 downstream task(node classification, clustering, link prediction)을 수행할 수 있다.
(거의 모든 representation learning이 그렇듯이, 고 차원으로 표현된 데이터를 저 차원으로 변환/압축하여 downstream task를 위한 준비를 할 수 있다.)
이러한 작업은 고정된 graph에서 embedding을 생성하는 것에 초점을 맞추고 있지만, 실 세계 application들은 관측되지 않은(unseen) node에 대해 embedding을 빠르게 계산하는 작업이 필요하다.
즉, 이런 inductive한 능력은 변화(진화/성장)하는 graph에서 동작하거나 지속적으로 unseen node를 마주치게 되는 ML system에선 필수적이며, node embedding을 생성하는 inductive한 접근법은 graph 간의 generalization이 보다 간편해질 수 있다.
즉, 단백질-단백질 상호작용(protein-protein interaction, PPI) graph에 대한 embedding generator를 train한 후, trained model을 활용하여 새로운 PPI graph에 대한 node embedding을 손쉽게 생성할 수 있다.
(Inductive method가 왜 필요한지에 대한 설명. model을 먼저 train 한 뒤, 다른 data에 대해 빠르게 embedding을 생성할 수 있다.)
그렇다면 왜 Inductive method가 transductive method보다 어려울까?
관측되지 않은(unseen) node를 일반화(generalize)하는데 있어, 설계한 알고리즘이 이미 최적화가 진행된 node embedding에 sub-graph를 할당하기 때문이다.
즉, node의 local role과 global position을 모두 나타내는 structural property를 인식하는 방법을 학습해야 한다.
(node embedding을 생성함에 있어 해당 node가 global한 관점에서 어떤 역할을 담당하는지, local한 관점에서 어떤 역할을 담당하는지를 고려해 적절한 embedding을 생성하는 것이 필요. node2vec에서 return parameter에 따라 local에 초점을 맞춰 embedding을 생성할지, global에 초점을 맞춰 embedding을 생성할지를 결정하는게 필요하다는 점에서 기인한 듯 하다.)
node embedding을 생성하는 작업은 선천적으로 transductive한 작업인데, 이는 matrix factorization 기반의 목적 함수를 사용해 각 node마다 embedding을 직접적으로 최적화 한다.
하지만 이 방법은 single/fixed graph의 node에 대해 prediction을 수행하므로 unseen data의 일반화를 잘 하지 못하는 문제가 있다.
DeepWalk에서 소개한 방법 처럼 inductive한 작업으로 변환할 수 있지만, 새로운 예측을 수행하기 전 추가적인 gradient descent 단계가 필요하기에 이는 굉장히 computationally expensive한 작업이 된다.
GCN처럼 convolution 연산을 이용해 graph의 구조를 학습하는 접근 법도 있지만, GCN은 fixed graph를 사용하는 transductive method에서만 사용되고 있다.
따라서 본 논문에서는 GCN을 inductive unsupervised learning으로 확장하고, GCN의 접근 방식을 일반화하여 trainable한 aggregate function을 사용하는 framework를 제안한다.
Present work
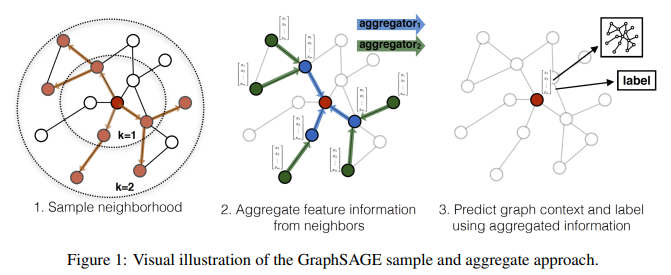
Inductive node embedding을 위한 general framework인 GraphSAGE(SAmple and aggreGatE)를 소개한다.
unseen node를 일반화하기 위한 embedding function을 학습하기 위해 node feature를 활용하며, 학습 알고리즘에 node feature를 활용함으로써 각 node마다 이웃의 topological structure 뿐만이 아닌 이웃 node에 존재하는 node feature의 분포 또한 학습이 가능하다.
또한 각 node마다 구별되는 embedding vector를 학습하는 대신, node의 local 이웃에서 feature 정보를 집계하는 aggregator function을 학습하며, 이 함수는 주어진 node로부터 몇 hop(depth)까지의 정보를 집계한다.
(aggregator function을 통해 한 node로 부터 $k$ 거리 만큼 떨어진 node의 정보를 활용. $k$ 거리 == $k$-hop)
test(inference)시엔 학습된 aggregator function을 활용해 unseen node 전체에 대한 embedding을 생성할 수 있다.
(즉 aggregator function이 정해진 hop 수 만큼까지의 node 정보를 집계하여 model train을 하고, trained model(aggregator function)을 이용해 unseen data에 대한 embedding을 간단하게 생성할 수 있다는 의미이다.)
Citation network, Reddit, PPI 총 3개의 dataset을 이용했을 때 기존 GCN의 단순한 aggregate 방식 보단 본 논문에서 제안한 여러 종류의 aggregator function이 embedding 생성에 있어 월등한 성능을 보여준다.
Related Work
(언제나 보는 선행연구 소개 & 우리 paper가 이래서 더 좋다~ 하는 내용들)
Factorization-based embedding approaches
random walk approach와 matrix-factorization 기반의 목적 함수를 이용해 low-dimensional embedding을 학습하는 연구가 존재한다.
이 방법들은 전통적인 spectral clustering, multi-dimensional scaling, PageRank와 유사하며, 각 node마다 직접적으로 node embedding을 학습하기에 기본적으로 transductive한 방법이고, 새로운 node에 대한 예측을 생성하기 위해 추가적인 training이 필요하다.
또한 이 방법들은 목적 함수가 embedding의 orthogonal transformation(직교 변환)에 대해 불변(invariant)한데, 이는 즉 embedding space가 graph마다의 embedding space를 자연스럽게 일반화하지 못함을 의미하며 re-train 동안 embedding space가 변경될 수 있다.
(train 마다 embedding space가 변할 수 있음을 이야기하는 듯 하다.)
Planetoid-I 알고리즘은 inductive & semi-supervised learning의 embedding 기반 접근법이지만, inference를 하는 동안 graph의 구조적인 정보(structural information)을 활용하지 않는다.
앞서 언급한 접근 방식들과는 다르게, 본 논문에서는 unseen node에 대한 embedding을 생성할 수 있도록 model train에 있어 feature information을 사용한다.
Supervised-learning over graphs
graph data의 supervised learning에 대한 여러 연구가 존재하며, 대표적으로 kernel-based 접근이 포함된다.
(graph의 feature vector가 다양한 graph kernel에서 부터 생성된다는 의미.)
WL graph kernel에 관한 내용은 다른 블로그 포스팅을 참고하면 좋을 듯 하다:
이 외에도 neural network를 활용한 접근 방안(최초의 GNN(2009), Recurrent-GNN 등)도 있었고, 본 연구는 해당 몇몇 알고리즘들에 영감을 받았다.
하지만 선행된 연구들은 graph(또는 sub-graph) classification에 초점을 두었고, 본 연구는 node 개별마다의 representation을 생성하는 것에 초점을 둔다.
Graph convolutional networks
CNN 구조를 사용하는 이 방법들은 large graph로 확장되지 않거나, graph classification (또는 둘 다)를 위해 설계되었다.
본 연구는 기본적으로 GCN에 기반하지만, GCN은 train 동안 full graph Laplacian을 알고 있어야 하는 문제가 있다.
(각 node마다 연결된 모든 node의 feature를 aggregate할 때 어느 node가 어느 node와 연결되었는지에 대한 연결 정보를 알고 있어야하므로.)
따라서 본 연구가 GCN을 inductive한 방법으로 확장한 것으로도 생각할 수 있다.
Proposed method: GraphSAGE
Embedding Generation (i.e. forward propagation) algorithm

입력: 전체 graph $\mathcal{G}$, 모든 node의 feature vector인 $\mathrm{x}_v$, 미분 가능한 집계 함수
$\mathrm{AGGREGATE_k}$, 이웃 함수 $\mathcal{N}$
출력: 모든 node에 대한 vector representation $\mathrm{z_v}$
line 1: 초기 representation 초기화
line 2~8: 탐색 깊이 $k$ ($k$-hop) 만큼 loop
line 3~6: 모든 node마다 loop
line 4: 현재 layer의 이웃 node들의 정보는 이전 layer에서 존재했던 이웃 node들의 정보를 집계 (이웃 representation 집계)
line 5: 현재 layer의 자기 자신 node의 정보는 이전 layer에서 존재했던 자신의 정보 & 현재 layer에서 앞서 계산한 이웃 node들의 정보를 집계 (이전 layer에서 계산된 자신의 representation & 현재 layer에서 계산된 이웃의 representation을 이용해 현재 layer에서의 자기 자신의 representation을 계산)
line 7: L2 normalization
model이 이미 train 되었다 가정하고, model의 parameter는 고정된 상태임을 가정한다.
$K$개의 집계 함수($\mathrm{AGGREGATE}$)는 이웃 node들로부터 정보를 집계하며, 가중치 행렬인 $\mathbf{W}$는 다른 layer(또는 다른 search depth)간 정보를 전파하는 역할을 수행한다.
각 iteration(각기 다른 search depth, hop) 마다 이웃 node의 정보를 집계, 이 과정을 반복, 반복하며 점점 더 많은 이웃 node들의 정보를 집계한다.
핵심을 살펴보면...
line 4: 각 node $v$는 근처 이웃 node의 representation을 단일 vector $\mathrm{h}^{k-1}_{\mathcal{N}_(v)}$로 집계한다.
이 과정은 이전 loop에서 생성된 representation에 의해 생성되며, $k=0$은 입력으로 전달된 초기 node feature를 의미한다.
line 5: 현재 자기 자신의 representation인 $\mathrm{h}^{k-1}_{v}$와 집계된 이웃 node들의 representation인 $\mathrm{h}^{k-1}_{\mathcal{N}_(v)}$을 CONCAT한다.
CONCAT한 vector를 non-linear activation function $\sigma$를 가진 fully-connected layer(FFN)로 전달한 후, 전달된 정보는 다음 step에서 사용될 representation이 된다.
놀랍게도 이게 전부다.
정해진 hop 수 $k$까지 각 node마다 이웃 node의 representation을 aggregate $\rightarrow$ 이전에 계산된 자신의 representation과 aggregate한 이웃 node의 representation을 CONCAT $\rightarrow$ 현재 자신의 representation을 계산
Relation to the Weisfeiler-Lehman Isomorphism Test
GraphSAGE는 기본적으로 graph 동형 테스트에 사용되는 classical한 알고리즘인 WL-test에 영감을 받았다.
위 Algorithm 1에서 다음의 가정을 한다면, 해당 알고리즘은 전형적인 WL-test의 예시가 된다.
- $K = |\mathcal{V}|$: 탐색 깊이를 node 수와 동일하게 설정.
- $\mathbf{W} = \mathbf{I}$: 가중치 행렬을 항등(Identity) 행렬로 설정.
- non-linearity를 가지지 않은 적절한 hash function을 aggregator로 설정.
(WL kernel/WL-test는 상단 Supervised-learning over graphs 문단에서 hyperlink로 설정한 블로그 포스팅 참고)
서로 다른 2개의 sub-graph에서 생성된 representation set $\mathrm{z}_v$가 동일하다면, WL-test에 따라 이 2개의 sub-graph는 isomorphic하다.
(즉 2개의 sub-graph에서 생성된 representation이 동일하다면 2개의 sub-graph는 동형사상.)
GraphSAGE는 WL-test의 continuous approximation으로, hash function을 trainable한 neural network aggregator로 대체한 셈이다.
Neighborhood definition
고정된 크기의 batch에서 계산 공간(computational footprint)을 유지하기 위해, 전체 이웃이 아닌 고정된 크기의 이웃 집합을 uniform하게 sample 한다.
$\mathcal{N}_(v)$는 고정된 크기의 집합인 {$u \in \mathcal{V} : (u, v) \in \mathcal{E}$} 로 부터 uniform하게 생성된 집합이며, Algorithm 1에서 각 $k$번째 iteration마다 서로 다른 sample을 수집한다.
실험적으로 보았을 때, $K=2$, $S_1 \cdot S_2 \leq 500$일때 최상의 성능을 보여주었다.
(즉 2-hop에 걸쳐 representation 계산을 위해 aggregate하는 이웃 node의 수가 총 500개 이하일 때 성능이 좋았다 라는 의미. (e.g. 1-hop에서 50개의 node를 sample($S_1 = 50$), 2-hop에서 10개의 node를 sample ($S_2 = 10$)))
논문 Appendix 부분에 sampling을 활용한 mimibatch training의 pseudocode가 같이 기술되어 있다.
Appendices A: Minibatch pseudocode (일부)

line 2~7: sampling 수행
line 9~15: forward propagation
앞서 소개되었던 Algorithm 1 부분에 sampling을 수행하는 과정이 추가되었다.
단순히 주어진 graph에서 node마다 정해진 hop 수 $k$만큼 까지 연결된 이웃 node들을 random하게 sampling 해서 batch를 생성한다. (forward propagation은 기존과 동일)
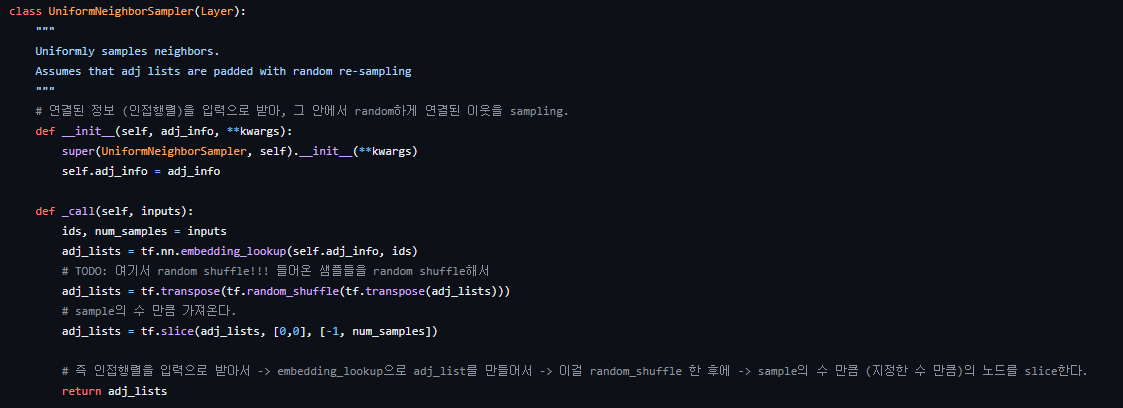
구현된 코드를 보면 random_shuffle 하여 num_samples 만큼 slice하며, graphsage/models.py에서 SampleAndAggregate class 내부의 sample 함수 부분을 보면 위 sampler를 활용한 sampling이 수행됨을 확인할 수 있다.
Learning the parameters of GraphSAGE
output representation $\mathrm{z}_u$에 대해 graph-based loss function을 사용하며, SGD를 이용해 가중치 행렬 $\mathbf{W}$와 aggregator function의 parameter tuning을 진행한다:

식1과 같은 CE-like loss function은 인접한 node는 유사한 representation을 갖도록 하고, 이질적인 node (feature가 극히 다른 node)의 representation은 최대한 구별되도록 하는 역할을 수행한다.
즉 $\log (\sigma(\mathrm{z}^{\top}_{u} \mathrm{z}_{v}))$ 부분이 1에 가까워지도록(비슷한 node는 비슷한 representation을 갖도록), $\log (\sigma(- \mathrm{z}^{\top}_{u} \mathrm{z}_{v}))$ 부분이 0에 가까워지도록(이질적인 node는 representation이 최대한 달라지도록) 목적 함수를 설정한다.
Aggregator Architectures
기존 N-D lattices(e.g. 이미지, 문장 등...)들을 이용해 train하는 ML과는 달리 node의 이웃들은 자연적인 순서가 없으므로, 따라서 aggregator function은 순서가 없는 모든 vector 집합에 대해 동작해야 한다.
즉, 이상적인 aggregator function은 trainable하고, 높은 representational capacity를 유지하면서 symmetric(입력의 순서가 바뀌어도 결과가 불변, invariant to permutation of its inputs)이어야 한다.
Mean Aggregator

단순히 $\mathrm{h}^{k-1}_{\mathcal{N}_(u)}, \forall u \in \mathcal{N}_(v)$에 있는 모든 vector들에 대해 element-wise mean을 계산하는 방법으로, 기존 transductive GCN의 convolutional propagation rule과 동일하다.
위의 식2를 Algorithm1의 line 4,5에 대입함으로써 inductive한 GCN 연산을 구현할 수 있다.
(기존의 GCN은 Algorithm1의 line 5에 해당하는 CONCAT 연산이 없음)
LSTM Aggregator
LSTM 구조에 기반한 aggregator로서, mean aggregator에 비해 더욱 큰 표현력(larger expressive capability)를 가질 수 있다.
하지만 기본적으로 LSTM은 입력을 순차적으로 처리하기 때문에 not symmetric (not permutation invariant)한데, 본 연구에서는 LSTM을 이웃 node들의 random permutation에 적용하여 unordered set에서 동작할 수 있도록 적용했다.
(해당 부분에 대한 commented source code)
Pool Aggregator

이는 symmetric하고 trainable하며, 각 이웃 vector는 독립적으로 fully connected neural network의 입력으로 전달되어 이웃 집합의 정보 집계를 위해 element-wise pooling 연산을 적용한다.
(이 방법은 일반적인 point set을 neural network에 적용한 PointNet[C. R. Qi, et al., CVPR2017]에서 영감을 받음)
MLP를 이웃 집합의 각 node representation에 대한 feature를 계산하는 여러 개의 함수 집합(set)으로 간주할 수 있으며, 계산된 feature에 pooling operator를 적용함으로써 model은 효과적으로 이웃 집합의 각기 다른 측면(aspect)을 포착할 수 있다.
Experiments
3가지의 benchmark task.
- citation dataset에 대한 classification
- reddit dataset에 대한 classification
- PPI dataset에 대한 classification.
(PPI의 경우 작은 크기의 graph가 다수 포함되어 있으므로, 해당 dataset에선 unseen graph에 대한 test를 수행)
Experimental setup
4개의 baseline.
- random classifier
- feature 기반의 logistic regression
- DeepWalk
- raw feature와 DeepWalk에서 생성된 embedding을 결합한 classifier
GraphSAGE가 GCN의 inductive한 방법이기에, GCN을 GraphSAGE-GCN으로 명명하여 비교 실험에 기재.
또한 aggregator function을 각기 달리 변형하여 사용하였고, $K=2$, $S_1=25$, $S_2=10$으로 설정.
(1-hop에서는 25개의 이웃 node를 sample, 2-hop에서는 10개의 이웃 node를 sample)
Inductive learning on evolving graphs: Citation and Reddit data &
Generalizing across graphs: Protein-protein interactions
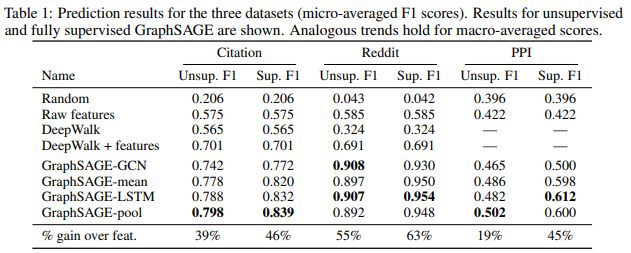
citation dataset에선 node degree를 feature로 사용하였고, abstract를 300-dimensional word vector로 변환하여 활용.
reddit dataset에서 node label은 subreddit(community)를 의미하며, 사전에 생성된 300-dimensional word vector를 feature로 활용.
PPI dataset에선 유전자의 위치 정보, 유전자의 생김새, 면역학적 특징(immunological signature)를 feature로 활용.
결과 table에서 볼 수 있듯이 inductive method인 GraphSAGE가 다른 baseline들에 비해 월등히 뛰어난 분류 성능을 보여줌을 알 수 있고, transductive method인 GCN(GraphSAGE-GCN)과 비교해도 대체적으로 좋은 분류 성능을 보여주는 것을 알 수 있다.
Runtime and parameter sensitivity

Deepwalk는 unseen node의 embedding을 계산하기 위해 SGD round를 새롭게 시작해야 하므로 속도가 많이 뒤쳐진다.
(Figure 2-A의 DW)
$K=1$로 설정한 경우에 비해 $K=2$로 설정한 경우가 10~15%의 성능 항상을 보이지만, $K=2$보다 크게 설정하는 경우 미미한 성능 차이(0~5%)를 보여준다.
(sample되는 이웃 node의 수 & hop 수를 적절하게 설정하는 경우 보편적으로 좋은 성능을 보인다.)
Summary comparison between the different aggregator architectures
LSTM, pool aggregator의 성능이 가장 좋게 나왔으며, 기존 GCN의 방법에 비해 대체적으로 논문에서 제안한 LSTM, pool, mean의 성능이 좋았다.
특이하게도 서로 다른 aggregator들을 사용한 결과에 대해 비모수 검정 기법인 Wilcoxon Signed-Rank Test를 진행하였고, T-통계량과 p-value가 applicable하였음을 확인하였다.
(또한 GCN 접근법에 비해 통계적으로 유의미한 gain을 얻었음을 한번 더 강조하였다.)
LSTM과 pool 간의 큰 성능 차이는 없었지만, 특성상 LSTM의 속도가 pool보다 (약 2배) 느렸음을 언급하였다.
Theoretical analysis &
Conclusion
GraphSAGE가 feature에 기반함에도 불구하고 graph의 구조를 학습할 수 있음을 소개하였고, 이웃 node의 sampling을 통해 runtime과 성능을 효율적으로 trade-off 할 수 있음을 보여주었다.
(Theoretical analysis와 Appendix 부분에 본 연구가 이론적으로 어떤 특징/강점이 있는지를 설명해주는데, 수학적인 background가 부족하여 별도로 기술하진 않았다😥)
개인적으로 GNN 연구를 할 때 GCN에 비해 여러 insight를 많이 가져다 준 논문이다.
neighborhood sampling을 소개하여 GNN의 mini-batch training이 가능함을 알려주기도 하였고, 이것이 발전하여 추후 layer-wise sampling, sub-graph sampling 등등 여러 sampler가 등장할 수 있게 하는 계기를 마련해주기도 했다는 생각이 든다.
실제로 PyG, DGL에서도 간단하게 sampler를 호출하여 random sampling을 수행할 수 있기도 하다.
하지만 이렇게 단순하면서도 편리하고 어떻게 보면 획기적인 neighborhood sampling의 (어떻게 보면 고질적인) 문제점이 있는데, 이는 추후 포스팅 할 글들에서 다시 언급하고자 한다.
22년 당시 review 후에 작성하였던 슬라이드도 함께 첨부하였다.
E.O.D.
'학업 이야기 > Paper Review' 카테고리의 다른 글
| Semi-Supervised Classification with Graph Convolutional Networks (2) | 2024.06.17 |
|---|