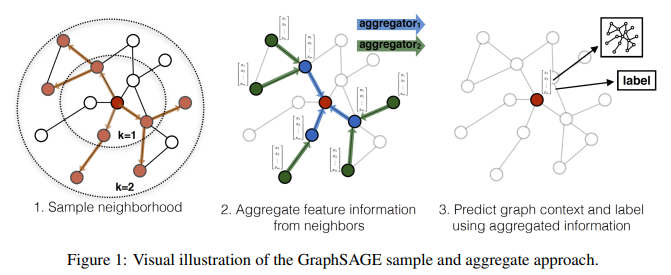
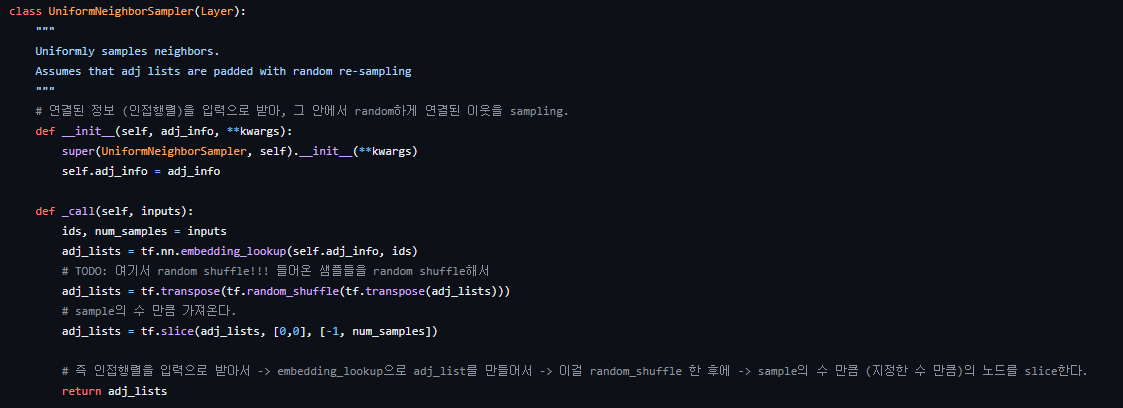
Preliminaries
지난번 포스팅에서 PyG의 mini-batch training을 위한 방법 중 하나인 NeighborLoader를 간략하게 살펴보았다.
이번엔 NeighborLoader와 간단한 dataset을 활용하여
이 neighbor sampling (또는 node-wise sampling)의 특징(?)을 알기 위해 간단하게 진행했던 실험에 대해 정리하고자 한다.
작성 편의상 sampling을 수행하는 기준 node, 즉 sampling을 수행하였을 때 최 상단에 위치하게 되는(기준이 되는) node를 anchor node로 작성하였다.
Cora dataset & EDA
여러 초장기 GNN paper에 자주 등장한 dataset이다.
PyG에선 torch_geometric.datasets.Planetoid 에 함께 포함되어 있다.(공식 doc 링크)
여러 GNN paper에 기재된 듯이, 비교적 작은 규모의 citation network 이다.
(전체 node의 수는 2708, edge 수는 5429, feature vector의 차원이 1433.)

그럼 그래프가 어떻게 생겼을까?
살펴보면 다음과 같다. (이미지 출처는 이미지에 포함)

직접 plotting해본 것도 있지만... 아무래도 이렇게 이쁘게 그려주신 분이 있다면 :)
추가적인 EDA를 위해 필요한 라이브러리를 import 한다.
import torch
import networkx as nx
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import pandas as pd
from torch_geometric.datasets import Planetoid
from torch_geometric.loader import NeighborLoader
from torch_geometric.seed import seed_everything
from torch_geometric.utils import to_networkx, unbatch_edge_index
seed_everything(62)
dataset = Planetoid(root='dataset', name='cora')
data = dataset[0]
del dataset
data.n_id = torch.arange(data.num_nodes)
각 node마다의 degree 정도/분포도를 확인.
graph = to_networkx(data)
degree_list = list(graph.degree)
df = pd.DataFrame(degree_list, columns=['n_id', 'degree'])
print(df['degree'].describe())
이미지로 봤던 graph에서 처럼, degree 분포가 상당히 극단적이다.
(근데 사실 대부분의 graph dataset들은 이런 식의 long-tail distribution인 경우가 많다.)
추가적으로 train mask, val mask, test mask 라는 것이 존재한다.
이는 각 train/val/test 마다 masking을 한 것으로, T/F로 이뤄진 값이며,
node를 unseen node처럼 간주하기 위해 사용하는 셈 이다.
print(sum(data.train_mask)) # 140
print(sum(data.val_mask)) # 500
print(sum(data.test_mask)) # 1000
train에는 140개의 mask가, val에는 500개의 mask가, test에는 1000개의 mask가 있다.
이게 도대체 무슨 의미가 있고, 왜 있는 걸까?
앞서 언급하였듯, Cora dataset은 데이터의 규모가 상당히 작은 편이다.
2708 node에 대해, mask를 적용하면 그 값이 False인 node를 train에서 제외하는 셈이다.
즉 해당 갯수(True인 갯수)의 노드만을 가지고 train/val/test를 실시한다는 의미로 볼 수 있다.
(적은 양의 data로 model의 충분한 generalizaion을 돕기 위해서 사용하는 셈 이라고도 볼 수 있을 듯.)

Mini-batch testing
GraphSAGE의 sampler가 어떻게 mini-batch를 생성하는지 직접 코드를 통해 확인해보자.
NUM_NEIGHBORS = [2,4] # 2-hop sampling
# NUM_NEIGHBORS = [-1] # 1-hop sampling
BATCH_SIZE = 16
INDEX_NUM = 0
loader = NeighborLoader(
data = data,
num_neighbors = NUM_NEIGHBORS,
batch_size = BATCH_SIZE,
input_nodes = data.train_mask, # "len(sum(data.train_mask)):140 / batch_size" 갯수 만큼의 batch가 만들어진다.
# directed=False, # RuntimeError: Undirected subgraphs not yet supported
disjoint=True # each seed node will create its own disjoint subgraph : 각 anchor node마다 disjoint한 sub-graph를 생성.
)
subgraph_list = []
nodes_in_subgraph = []
edges_in_subgraph = []
for batch in loader:
subgraph_list.append(batch)
# 해당 배치에서 anchor node 를 제외하고 새로 sampling된 node
nodes_in_subgraph.append(len(batch.n_id.tolist()) - BATCH_SIZE)
# 새로 sampling된 노드들과 anchor node들 간의 connectivity
edges_in_subgraph.append(batch.edge_index.numpy()[1].shape[0])
print('Total # of batches : ', len(subgraph_list)) # 9
loader에 대한 loop을 실행할 때 실질적인 sampling이 수행된다.
여기서, disjoint=True 를 하면 서로 연결된 anchor node끼리는 computation graph에 포함시키지 않는다.
즉, anchor node끼리 겹치지 않으며 anchor node 1개당 고유한 computation graph를 생성하게 되고,
약간의 작업을 통해 batch안에 있는 computation graph들을 각각 분할시킬 수 있다.
(당시 공식 repo discussion 탭에서 질문했던 내용: https://github.com/pyg-team/pytorch_geometric/discussions/6325)
그럼 batch 안에 들어가는 실제 computation graph는 어떻게 생성되는지 확인해보자.
sample_batch = subgraph_list[INDEX_NUM]
# edge_batch = sample_graph[sample_graph.edge_index[0]]
# print(sample_graph.edge_index[0]) # source->target 에서 target에 해당하는 index만을 챙기기.
### batch vector에서 실제로 어떤 node가 어떤 sub-graph에 할당되어 있는지 확인.
### 즉, 기존 edge_index랑 이 값이랑 비교하면 어떤 앵커가 몇개를 샘플링했는지 확인가능.
# print(sample_batch.edge_index.numpy())
# print(sample_batch.batch[sample_batch.edge_index[0]].tolist())
# batch안에 있는 개별 anchor node마다의 computation graph를 추출할 수 있음.
sample_graph_edge_index = sample_batch.batch[sample_batch.edge_index[0]]
for i in range(BATCH_SIZE):
edge_index_for_i = sample_batch.edge_index[:, sample_graph_edge_index == i]
print(edge_index_for_i.numpy())
print된 결과물(첫번째 batch에 포함된 computation graph들)을 보면 다음과 같다.

모든 node마다 2-hop sampling을 수행하였고, 1-hop에서는 2개의 node를, 2-hop에서는 4개의 node를 sampling 했다.
앞서 수행했던 data.n_id = ~~ 부분을 통해 edge_index에 있는 값 (0~15)과 실제 graph에서의 id값인 n_id의 매칭을 통해 각 배치마다 어떤 node가 computation graph를 어떻게 형성하는지 확인 가능하다.
앞서 지정한 BATCH_SIZE 개수 만큼의 computation graph가 생성된 것을 확인할 수 있는데,
눈여겨 볼 점은 각 computation graph마다의 크기가 다른 점이다.
상단 Cora dataset의 graph plot을 봐도 알 수 있듯, 각 node의 degree가 long-tail distribution의 형태를 따르고 있기에
sampling을 수행할 때 고립된(isolated) node가 있다면 서로간의 sampling만을 수행하고 종료되는 것을 짐작할 수 있다.
그렇다면 무엇이 문제일까?
비교분석을 위해 간단한 코드를 작성해서 chart로 확인을 해보자.
# ## x축은 각 batch id, y축은 그 길이 값 -> bar chart
graph_info_tuples = list(zip(nodes_in_subgraph, edges_in_subgraph))
df = pd.DataFrame(graph_info_tuples, columns=['node_num', 'edge_num'])
ax = df.plot(kind='bar', rot=0, xlabel='batch_id', ylabel='value', title=f'batch_size={BATCH_SIZE} \n num_neighbors={NUM_NEIGHBORS}', figsize=(12, 8))#, cmap=cmap)
df.plot(kind='line', xlabel='batch_id', ylabel='value', ax=ax)#, cmap=cmap)
for c in ax.containers:
ax.bar_label(c, fmt='%.0f', label_type='edge')
ax.margins(y=0.1)
ax.legend(title='columns', bbox_to_anchor=(1, 1.02), loc='upper left')
plt.show()
먼저 batch_size를 다르게 (batch마다 들어가는 anchor node 수를 다르게) 한 경우를 살펴보면 다음과 같다.



batch마다 들어가는 anchor node 수를 다르게 한 경우, 한 개 batch마다의 전체 computation graph들의 크기가 증가하는 경향을 볼 수 있다.
즉, batch_size를 크게 잡으면(한 batch에 넣을 anchor node수를 늘리면) 1개 batch당 computation graph 수 증가하게 되고, batch당 계산량의 차이가 더 심해질 수 있다.
다음은 num_neighbors를 다르게 (고려하는 hop을 다르게, 고려하는 이웃 수를 다르게) 한 경우는 다음과 같다.

고려하는 hop 수를 늘리거나, 고려하는 이웃의 수를 늘리는 경우 (앞서 살펴본 경우와 비슷하게) 한 개 batch마다의 전체 computation graph의 깊이/크기 차가 심하게 증가하는 경향을 확인할 수 있다.
즉 batch당 computation graph의 깊이(depth)/크기가 증가하는 것을 확인할 수 있고, 그 차이의 폭(gap)이 더욱 커지는 것을 바로 확인할 수 있다.
특히 위 사진의 3사분면과 4사분면에서 그 차이가 가장 크게 두드러지는 것을 확인할 수 있는데,
고려하는 이웃의 수가 많으며 고려하는 hop 수가 늘어남에 따라 computation graph의 깊이/크기가 지수적으로 폭발하는 현상을 neighborhood explosion이라고 한다.
(여러 paper에서 언급되는 용어 이기도 하고, PyG 공식 docs에서도 간략하게 소개하고 있다.)
Consideration
neighborhood sampling은 random sampling을 통해 정말 간단하면서도 상당히 안정적인 mini-batch training을 가능하게 한다.
하지만 앞서 진행한 간단한 mini-batch test를 통해 확인한 것 처럼, 무턱대고 sampling을 수행하게 되면 batch마다의 computation graph 크기가 달라지게 되고, neighborhood explosion 문제가 발생할 수 있다.
그렇다면 이게 왜 문제가 될까?
실제 산업현장이 아닌 이상, 대부분 single GPU로 시간을 들여서 이런 문제는 충분히 커버할 수 있는 수준일 것이다.
(위처럼 Cora 같은 dataset이나, Reddit 같은 dataset이라면...)
하지만 실제 산업현장(실세계, real world)에서 등장하는 대부분의 데이터들은 규모가 정말 방대한 경우가 많고,
single GPU로는 턱 없이 부족한 경우가 많다.
(당장 Jure 교수님 산하의 stanford 팀에서 개발/운영중인 OGB(Open Graph Benchmark)를 봐도 large-scale challenge가 있고, 제공중인 dataset에도 상당히 큰 규모의 dataset이 있다.)
결국 Multi-GPU를 통한 distributed training이 필요한데, 보다시피 graph data의 특성 상 이게 상당히 힘들다.
(즉 large graph로부터 mini-batch를 어떻게 잘 만들 것 인지가 문제.)
GPU마다의 load balance를 맞추기 위해선 각 GPU마다 담당하는 양, 계산량이 비슷해야 synchronize가 잘 되어서 이상적인 distributed training이 될 것인데...
앞서 보았듯, mini-batch 마다 그 안에 들어있는 graph data의 크기가 제각각이니 synchronization도 잘 이뤄지지 않게 되고, GPU마다 계산량이 달라지게 되며 결국 놀게되는 GPU가 생겨날 수 밖에 없다.
(이렇게 놀게되는 GPU가 생겨서 작업 시간이 비효율적?이게 되는 문제를 straggler problem이라고도 한다.)
결국 mini-batch를 어떻게 잘 만들어 볼 것이냐 가 관건일 것인데, 단순히 GraphSAGE에서 제안한 random sampling 만으로는 mini-batch를 어떻게 적절하게 잘 만들기가 상당히 골치아프다는 점을 짚고 넘어갈 수 있다.
Conclusion
물론 다양한 paper들이 large-scale graph를 어떻게 효율적으로 distributed training 할 수 있는지 그 방법을 제안하기도 했고, Tiktok의 개발사?로도 알려진 ByteDance에서도 관련된 paper를 내기도 했다.
(당시 review했던 paper들은 기회가 된다면 천천히 posting 하는 것으로...)

글을 작성하며 예전 notion에 정리했던 내용들을 천천히 다시 둘러보니... 참 여러 생각이 든다.
돈 한푼 없이 정말 말 그대로 재미?로 시작해서, 다른 연구실 분과 협업도 해보고, 실험을 하면서 이런 현상이/문제가 정말로 있구나 하는걸 직접 확인하고, (비록 국내 학술대회 였지만) 첫 논문도 작성해보고...
단지 프로젝트가 상당히 길어질 것 같아 3학기를 마친 후 방학때 물러나게 되었지만, 기회가 된다면 다시 한번 진득하게 보고 싶은 field 이기도 하다.
지금은 뭐... 연구실의 다른 후배 분이 이어서 해주시고 있는지, 프로젝트가 그냥 무산났을지도 모르겠다.
당시에도 연구실에서 이 프로젝트를 하던 인원이 나 밖에 없었고, 4학기때 새로 들어온 후배 분에게 간략?한 인수인계를 해드리긴 했는데... 어떻게 진행중인지는 ^^;;
이전 PyG 포스팅 이후 딱 하반기 시즌이 열리는 바람에 하반기에 참 치이고 데이고,
정신없이 지내다가 한숨 돌리고 다시 기록해둬야지 하고 보니 어느새 거진 반년이 지나버리긴 했지만..
마음 속 응어리가 조금이나마 줄어든 기분은 든다. :)
다음 번 이쪽(Programming) 포스팅이 아...마 있을지는 잘 모르겠지만, 포스팅을 하게 된다면 당시 비교실험 등 을 진행했던 코드를 작성하며 review 해보고자 한다.
(집의 환경이 multi-GPU가 아니기에, 아마 single-GPU 코드를 작성하게 될 것 같긴 하다.)
E.O.D.
'학업 이야기 > Programming' 카테고리의 다른 글
| PyTorch Geometric(PyG) - NeighborLoader (3) | 2024.08.26 |
|---|---|
| PyTorch Geometric(PyG) 개요 (0) | 2024.08.05 |